在这春暖花开之时，武汉终于按下了重启键。4月8日起，武汉市解除离汉通道管控措施，有序恢复对外交通，也标志着武汉的经济社会活动按下“重启键”。与此同时，气温也越来越高，这是不是意味着新冠已经离我们远去了？钟南山院士说了，现在还不是摘口罩的时候！当下，疫情防控已经常态化，和病毒的鏖战是一场持久战，打起精神坚持下去，迎来真正过关的时刻！！

     勤洗手，戴口罩，少聚集，为什么仍是我们在复工复产复课时要坚持执行的？下面我们将利用TI模拟社交活动，来给大家展示做好防护和居家隔离的重要性。

在此之前，我们先了解两个名词：

基本传染数R0 

在流行病学上，指在没有外力介入，同时所有人都没有免疫力的情况下，一个感染到某种传染病的人，会把疾病传染给其他多少个人的平均数。

Flattening the Curve 

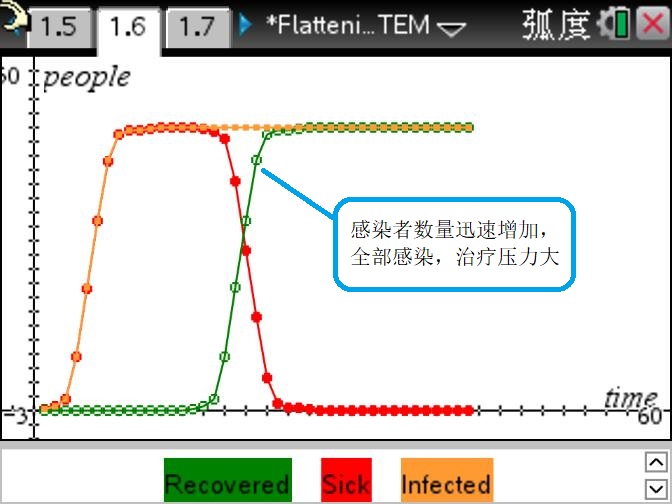
是针对疫情快速爆发情况下提出的一种控制措施。这里的curve（曲线），指的是疫情初期在没有采取相应控制手段的情况下，感染病例（人数）迅速上升的陡峭曲线。这个曲线一旦超出某个国家现有的医疗能力水平线（床位、医护人员、药品等），便会使得局势更为快速地恶化。

 蒙特卡罗模拟建模描述了在一个群体中，受感染者（红色）与未感染者（黑色）是如何相互作用的。R0表示二者相遇而导致感染的机率，当R0的设置值较低时，大多数接触不会导致感染；当R0的设置值较高时，大多数接触会导致感染。“社交融合”是一种群体行为，如航空旅行，它会影响日均接触的次数。“自我隔离”是将健康个体与疾病个体隔离的一种群体行为，但自我隔离不能保证同一家庭的人不受感染。这个模拟模型假设每位感染这种疾病的人会在14天后康复。

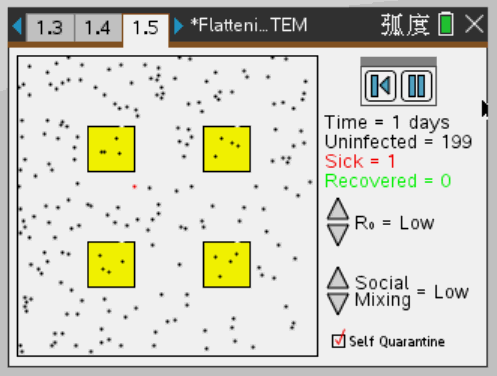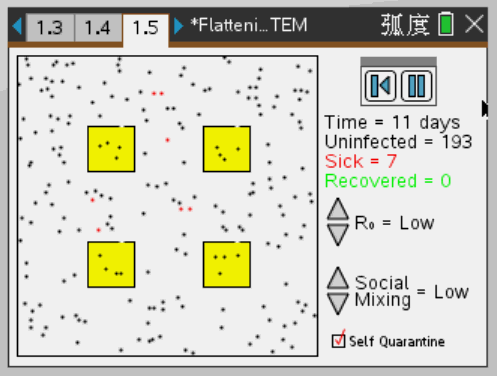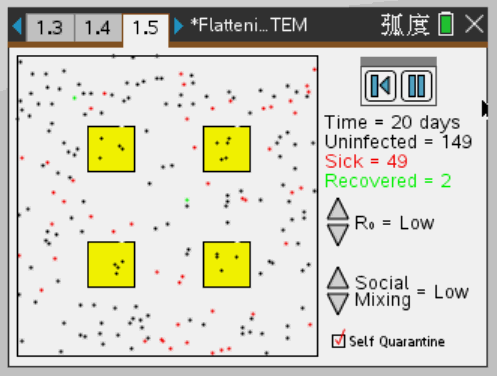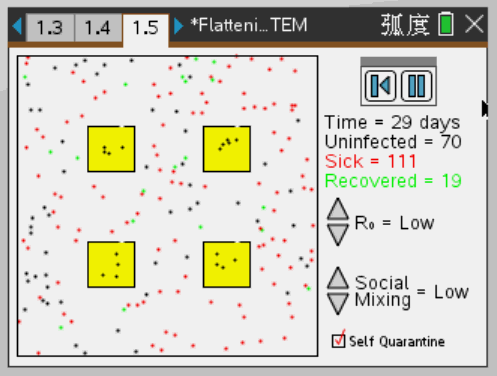
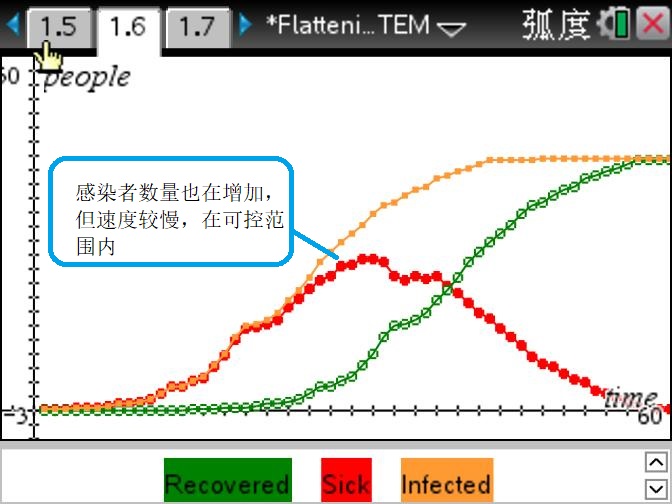
      由图可以看出，做好防护，居家隔离，使疫情的传播速度减缓，不会再短期内爆发。这样一来，即使最终受感染人数不变，也能使病例曲线扁平，拉长，争取更多的时间准备医疗资源，研制攻克病毒的方案。